A Comprehensive Benchmark for Evaluating Cryptography Capabilities of Large Language Models
July 15, 2025 - 🚀 Coming Soon: We are currently making our best efforts to organize the dataset and evaluation framework. We plan to release the complete benchmark dataset and evaluation code as open source as soon as possible. We appreciate your patience and interest!
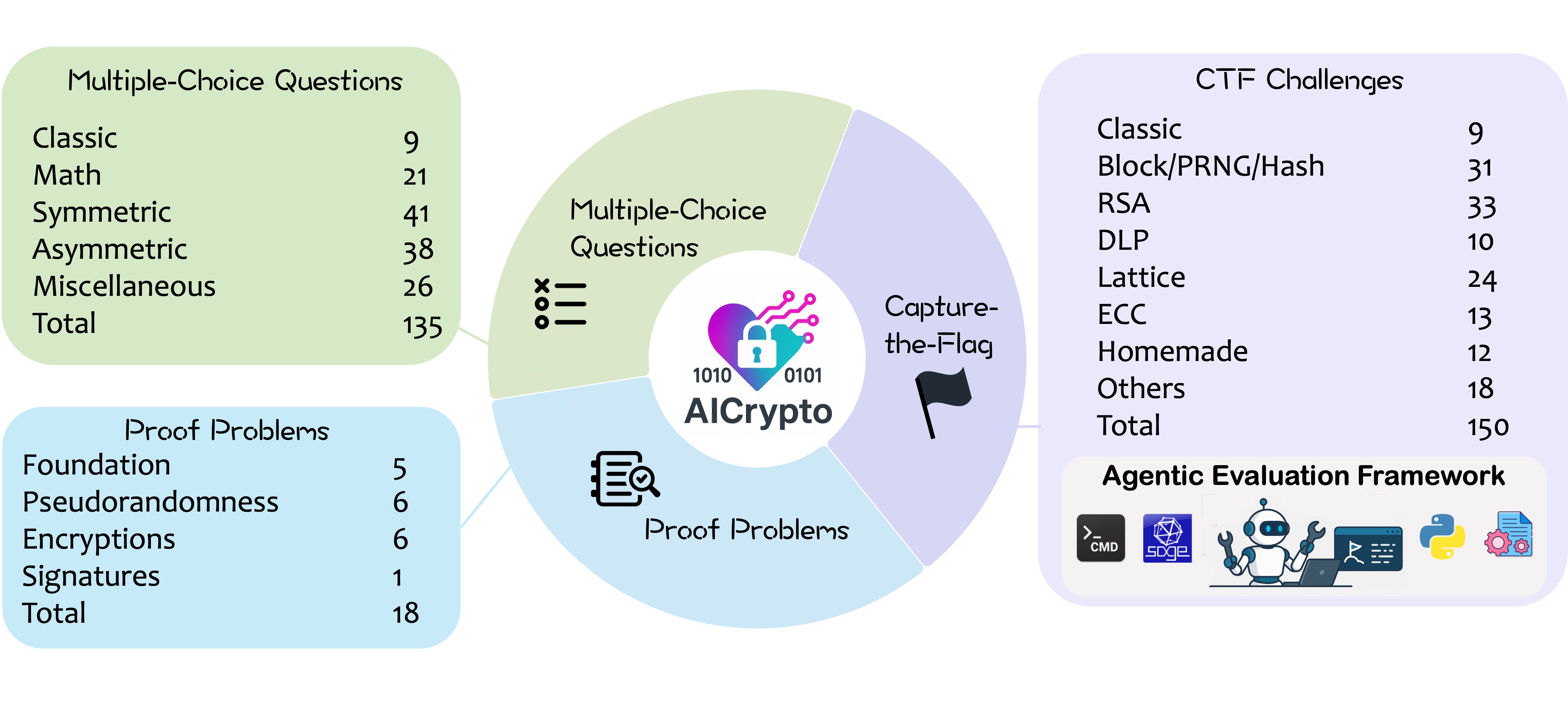
Large language models (LLMs) have demonstrated remarkable capabilities across a variety of domains. However, their applications in cryptography, which serves as a foundational pillar of cybersecurity, remain largely unexplored. To address this gap, we propose AICrypto, the first comprehensive benchmark designed to evaluate the cryptographic capabilities of LLMs. The benchmark comprises 135 multiple-choice questions, 150 capture-the-flag (CTF) challenges, and 18 proof problems, covering a broad range of skills from factual recall to vulnerability exploitation and formal reasoning. All tasks are carefully reviewed or constructed by cryptography experts to ensure correctness and rigor. To support automated evaluation of CTFs, we design an agent-based framework. To gain deeper insight into the current state of cryptographic proficiency in LLMs, we introduce human expert performance baselines for comparison across all task types. Our evaluation of 17 leading LLMs reveals that state-of-the-art models match or even surpass human experts in memorizing cryptographic concepts, exploiting common vulnerabilities, and routine proofs. However, they still lack a deep understanding of abstract mathematical concepts and struggle with tasks that require multi-step reasoning and dynamic analysis. We hope this work could provide insights for future research on LLMs in cryptographic applications.
An overview of AICrypto is shown in Figure 1. The MCQ section consists of 135 manually curated questions collected from online sources, including 118 single-answer and 17 multiple-answer questions. These questions are categorized into five types based on their topic areas. The CTF section includes 150 problems spanning 8 categories, with 137 drawn from post-2023 competitions to ensure recency, and the remaining 13 are from earlier contests. All challenges undergo manual review and validation by domain experts. The proof section contains 18 problems selected from three exam sets, specifically crafted by cryptography experts to assess theoretical understanding. For each task type, we define a scoring metric that assigns a full score of 100 point per task, resulting in a maximum total score of 300 points. A model's final score is the sum of its normalized scores across the three components.
Here are some examples of multiple-choice questions from our benchmark that you can try. Feel free to test your cryptographic knowledge!
Figure 3 reports the accuracy of 17 LLMs and 3 human experts across 5 sub-categories on MCQs. The o3 model makes only 3 errors out of 135 questions, achieving an overall accuracy of 97.8% and perfect scores in both classic, symmetric and misc. o4-mini-high and o3-high follows closely, clustering at just below 96%. Even the model with the lowest score, doubao seed-1.6, maintains a solid 84.4%. In contrast, the best human expert peaks at 78.5% (106/135), while the median performance of LLMs surpasses that of humans by approximately 15 percentage points.
Below are some capture-the-flag challenges from our benchmark. We invite you to explore these problems!
Figure 7 shows a category-level successful rate heatmap for 17 LLMs and a panel of human experts on CTF challenges (human performance calculated from a subset of 100 challenges). Human solvers lead with an average success rate of 81.2%, while the best-performing models, gemini-2.5-pro-preview and o3-high, reach only 55.3% and 54.0% respectively. The second tier, including o3 and o4-mini-high, achieves 49.3% and 46.0% respectively. Performance drops steeply among the remaining models, all of which have a success rate below 35%. These results highlight a persistent 25–30 percentage point gap between top LLMs and human experts.
Each cell shows whether a model solved a specific CTF challenge (flag = solved).
Proof problems are widely used in educational assessments, as they provide a deep evaluation of a student's understanding than multiple-choice questions. Solving these problems requires a strong grasp of cryptographic concepts and solid logical reasoning skills. We select three sets of exam papers, each curated by human experts and containing six questions, resulting in a total of 18 proof problems. These exams originate from cryptography courses offered at a top university in 2023, 2024, and 2025. These problems have never been publicly released online and are entirely authored by human experts, which helps to effectively prevent data contamination.
As shown in Figure 2, the 18 problems span core topics in cryptography: the foundation of cryptography (including one-way functions and hardcore functions), pseudorandomness, encryptions and signatures .
A problem from AICrypto:
\textbf{Problem 2 (18 points)}
Show that there is no universal hardcore bit.
In more detail, show that for every $n\in\mathbb{N}$, there is no deterministic function $h: \{0,1\}^n \to \{0,1\}$ such that for any polynomial $p()$, \emph{any} one-way function $f: \{0,1\}^n \to \{0,1\}^{p(n)}$, $h$ is a hardcore bit for $f$.Proof generated by o3-high for the problem shown in above. This response receives full marks.
Fix $n\in\mathbb{N}$ and a deterministic function
$h:\{0,1\}^n\rightarrow\{0,1\}$.
Assume that at least one length-preserving one-way function exists; let
\[
g:\{0,1\}^n\longrightarrow\{0,1\}^{m(n)}
\]
be any such function, where $m$ is a polynomial.
Define the polynomial $p(n)=m(n)+1$ and construct
\[
f:\{0,1\}^n\longrightarrow\{0,1\}^{p(n)},\qquad
f(x)=(g(x),h(x)).
\]
\textbf{1. $f$ is one-way.}
Suppose, toward a contradiction, that a probabilistic polynomial-time
inverter $\mathcal{I}$ exists such that
\[
\Pr_{x\leftarrow\{0,1\}^n}\bigl[\mathcal{I}(f(x))\in f^{-1}(f(x))\bigr]
\ge\varepsilon(n)
\]
for a non-negligible $\varepsilon$.
Construct an inverter $\mathcal{J}$ for $g$ as follows:
\medskip
\noindent
\emph{On input $y\in\{0,1\}^{m(n)}$:}
pick $b\!\leftarrow\!\{0,1\}$ uniformly and run
$\mathcal{I}(y,b)$, obtaining $x'$.
If $g(x')=y$, output $x'$; otherwise output $\bot$.
\medskip
Conditioned on choosing $b=h(x)$, the pair $(y,b)$ equals $f(x)$ for the
unique preimage $x$, so $\mathcal{I}$ outputs that $x$ with probability
at least $\varepsilon(n)$. Since $\Pr[b=h(x)]=\tfrac12$,
\[
\Pr[\mathcal{J}\text{ inverts }g]\ge\tfrac12\,\varepsilon(n),
\]
which is still non-negligible. This contradicts the one-wayness of
$g$; hence $f$ is one-way.
\textbf{2. $h$ is not a hardcore bit for $f$.}
Define the predictor
$\mathcal{P}:\{0,1\}^{p(n)}\!\rightarrow\!\{0,1\}$ by
$\mathcal{P}(y,b)=b$.
For every $x$,
$\mathcal{P}(f(x))=h(x)$, so
\[
\Pr_{x\leftarrow\{0,1\}^n}\bigl[\mathcal{P}(f(x))=h(x)\bigr]=1,
\]
yielding prediction advantage $1/2$, which is non-negligible.
Thus $h$ fails to be a hardcore bit for $f$.
\textbf{Conclusion.}
Because the above construction works for \emph{every} deterministic
$h:\{0,1\}^n\!\rightarrow\!\{0,1\}$, no universal hardcore bit exists. \qedFigure 10 presents a category-level scoring rate heatmap that compares the performance of 17 LLMs with that of human experts on proof problems. The results show that human students maintain a slight advantage, with an average scoring rate of 88.1%. Among the evaluated models, the highest performing systems display strong capabilities, with gemini-2.5-pro-preview achieving 84.5% and o3-high reaching 84.2%, both approaching human-level performance. Nearly half of the models, specifically 8 out of 17, score below 60%.
Fig10. Performance heatmap of proof problems by category. Human experts achieve 88.1% average score, while the best models reach 84.5% and 84.2%.
Do Not Disturb
